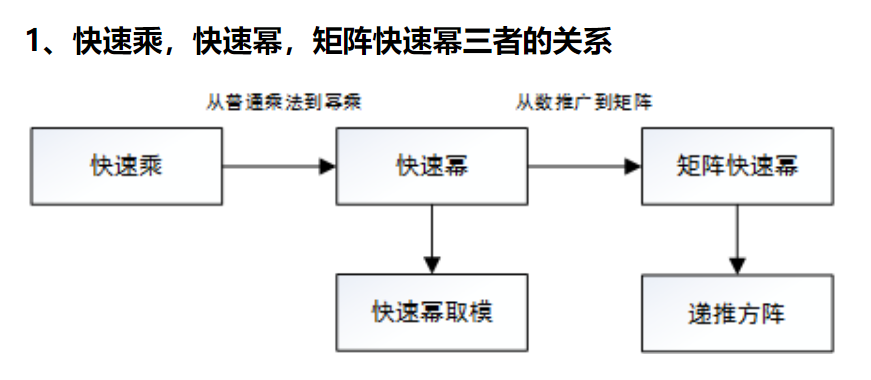
下面说的都是一次递归公式,其他的例如像Quadratic Map这种二次递归,不一定有通项公式,不能用矩阵快速幂实现快速运算,得老老实实用递归或者渐进表达式。
斐波那契数列
定义
\(a_n = a_{n-1} + a_{n-2}\),其中 \(a_0 = 1\),\(a_1 = 1\)
矩阵变换
\(\begin{bmatrix} a_n \\ a_{n-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_{n-1} \\ a_{n-2} \end{bmatrix}\)
代码
from sage.all import *
state = [1, 1]
for i in range(1, 10**2+1):
y = state[i] + state[i-1]
state.append(y)
M1 = matrix([
[1, 1],
[1, 0],
])
M2 = matrix([
[state[1]],
[state[0]],
])
state_ = (M1**(10**2) * M2)[0][0]
print(state_ == state[-1])一阶线性递推式
定义
\(f_n \equiv a \times f_{n-1} + b \mod{p}\)
矩阵变换
\(\begin{bmatrix} f_n \\ b \end{bmatrix} = \begin{bmatrix} a & 1 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} f_{n-1} \\ b \end{bmatrix}\)
代码
from sage.all import *
from Crypto.Util.number import getRandomInteger
state = [getRandomInteger(256)]
a = getRandomInteger(256)
b = getRandomInteger(256)
p = getRandomInteger(256)
for i in range(10**2): # 10**10000
y = (a * state[i] + b) % p
state.append(y)
M1 = matrix(Zmod(p), [
[a, 1],
[0, 1],
])
M2 = matrix(Zmod(p), [
[state[0]],
[b],
])
state_ = (M1**(10**2) * M2)[0][0]
print(state_ == state[-1])二阶线性递推式
定义
\(f_n \equiv a \times f_{n-1} + b \times f_{n-2} + c \mod{p}\)
矩阵变换
\(\begin{bmatrix} f_n \\ f_{n-1} \\ c \end{bmatrix} = \begin{bmatrix} a & b & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} f_{n-1} \\ f_{n-2} \\ c \end{bmatrix}\)
代码
from sage.all import *
from Crypto.Util.number import getRandomInteger
state = [getRandomInteger(256), getRandomInteger(256)]
a = getRandomInteger(256)
b = getRandomInteger(256)
c = getRandomInteger(256)
p = getRandomInteger(256)
for i in range(1, 10**2+1): # 10**10000
y = (a * state[i] + b * state[i-1] + c) % p
state.append(y)
M1 = matrix(Zmod(p), [
[a, b, 1],
[1, 0, 0],
[0, 0, 1],
])
M2 = matrix(Zmod(p), [
[state[1]],
[state[0]],
[c],
])
state_ = (M1**(10**2) * M2)[0][0]
print(state_ == state[-1])转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以邮件至 skatexu@qq.com