函数图像
sin
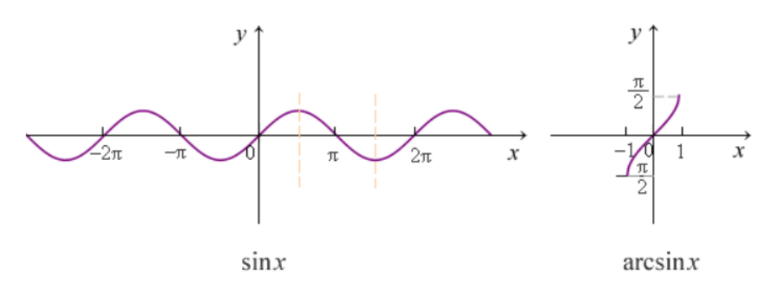
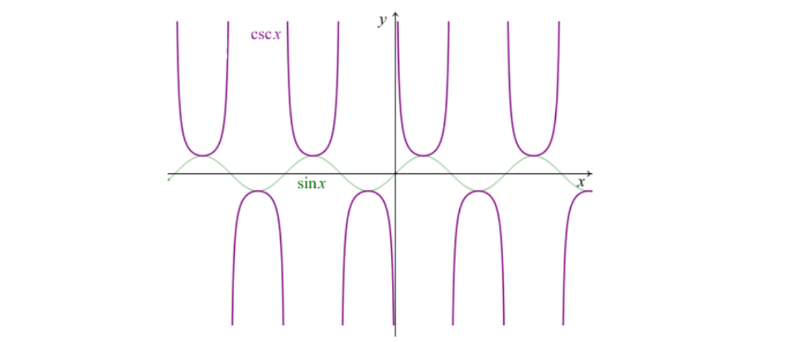
cos
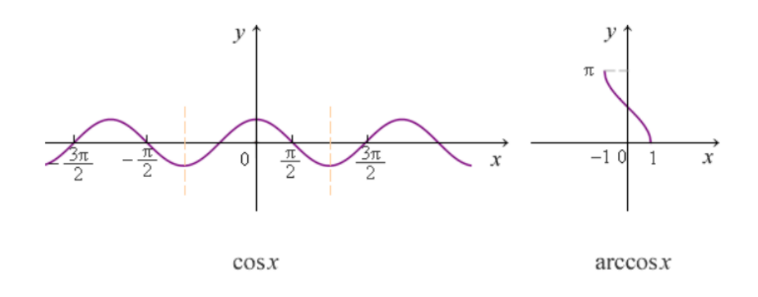
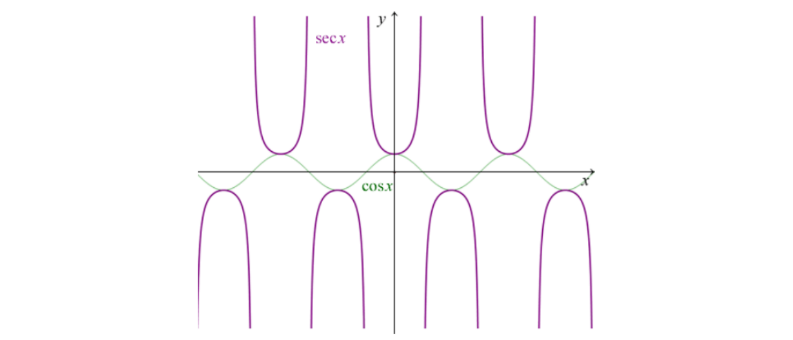
tan
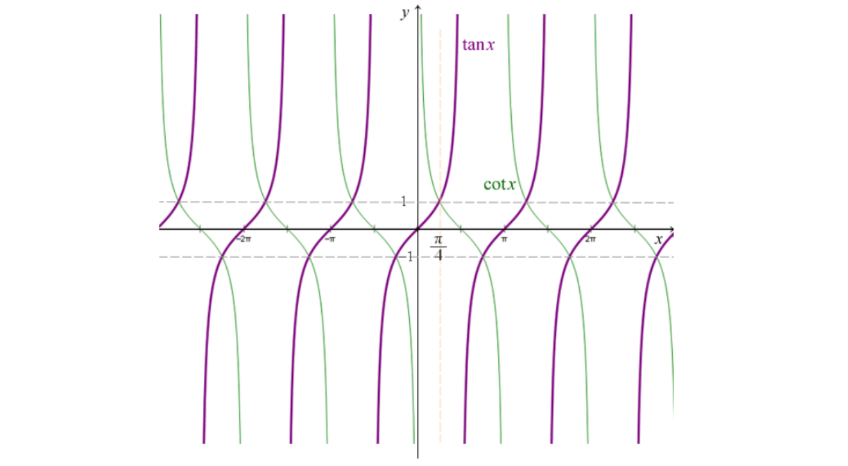
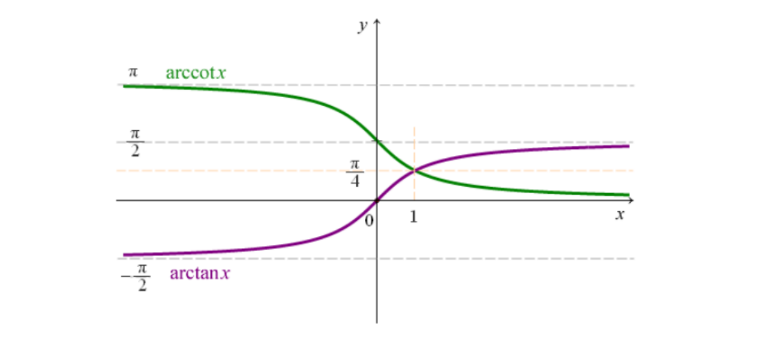
基本公式
倒数关系
\(\sin{x}\csc{x}=1\)
\(\cos{x}\sec{x}=1\)
\(\tan{x}\cot{x}=1\)
商数关系
\(\tan{x}=\dfrac{\sin{x}}{\cos{x}}\)
平方关系
\(\sin^{2}{x}+\cos^{2}{x}=1\)
\(\tan^{2}{x}+1=\sec^{2}{x}\)
\(\cot^{2}{x}+1=\csc^{2}{x}\)
诱导公式
公式1~5
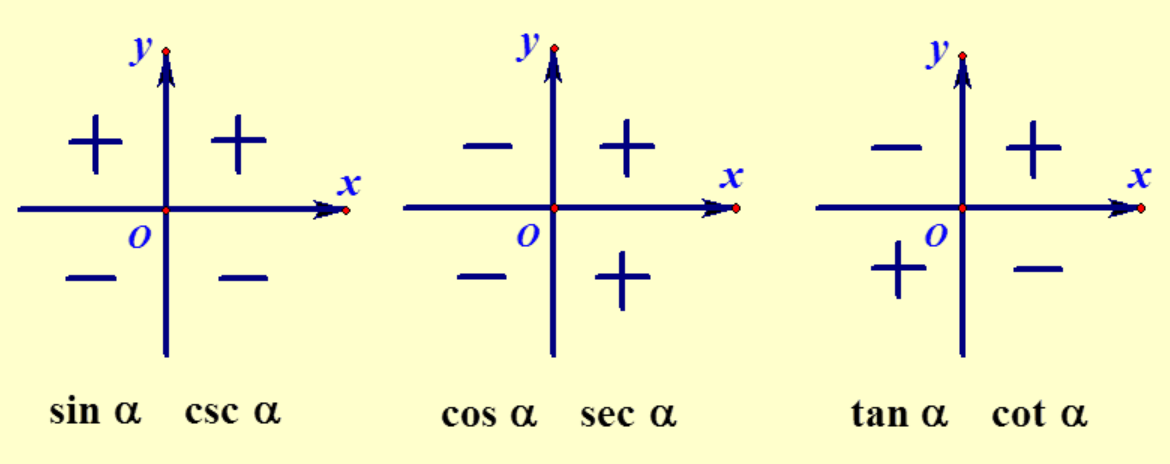
\(\sin(n\pi+x)=(-1)^n\sin{x}\)
\(\cos(n\pi+x)=(-1)^n\cos{x}\)
公式6
\(\cos(\dfrac{\pi}{2}+x)=-\sin{x}\)
推导公式
和差化积
令 \(t_1=\dfrac{a+b}{2}\),\(t_2=\dfrac{a-b}{2}\)
\(\sin{a}+\sin{b}=2\sin{t_1}\cos{t_2}\)
积化和差
令 \(t_1=a+b\),\(t_2=a-b\)
\(\sin{t_1}+\sin{t_2}=2\sin{a}\cos{b}\)
二角和差
\(\sin(a\pmb)=\sin{a}\cos{b}\pm\cos{a}\sin{b}\)
\(\cos(a\pmb)=\cos{a}\cos{b}\mp\sin{a}\sin{b}\)
\(\tan(a\pmb)=\dfrac{\tan{a}\pm\tan{b}}{1\mp\tan{a}\tan{b}}\)
二倍角
\(\sin{2x}=2\sin{x}\cos{x}\)
\(\begin{aligned} \cos{2x} &=\cos^2{x}-\sin^2{x}\\ &=2\cos^2{x}-1\\ &=1-2\sin^2{x} \end{aligned}\)
万能代换
令 \(t=\tan{\dfrac{x}{2}}\)
\(\sin{x}=\dfrac{2t}{1+t^2}\)
\(\cos{x}=\dfrac{1-t^2}{1+t^2}\)
\(dx=\dfrac{2}{1+t^2}dt\)
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以邮件至 skatexu@qq.com